aaaaaa.... q nervosooo!!!
10 Paradoxos para deixar seu cérebro ocupado por algum tempo
Quando o assunto é resolver mentalmente problemas, a lógica e o bom senso são grandes aliados. Com a ajuda deles, conseguimos encontrar a melhor solução para que cheguemos ao resultado desejado. Porém, existem os paradoxos, que são aqueles dilemas capazes de desafiar nosso cérebro ao nos colocar diante de questões que mais parecem um labirinto.
Neste post, o Incrível.club traz para você uma lista dos mais conhecidos paradoxos da história. Nossa intenção é que você coloque seu cérebro para treinar pesado!
1. Paradoxo dos corvos

Também é conhecido como “paradoxo da negação”, e foi proposto pelo filósofo Carl Hempel. Seu objetivo era provar que, quando os acontecimentos coincidem ao longo do tempo com o definido por uma teoria, nossa confiança naquela teoria aumenta. Para ilustrar seu argumento, ele usou como exemplo a teoria de que “todos os corvos são pretos”.
Se analisarmos milhões de corvos, observando que todos são da cor preta, acreditaremos cada vez mais na teoria segundo a qual “tudo que não é preto não é corvo”. Ao observar uma maçã vermelha que, por não ser preta, é um “não-corvo”, a convicção de que todos os corvos são pretos é maior.
2. Paradoxo de Epimênides

Em Creta, na época da Grécia Antiga, um homem chamado Epimênides de Cnossos dizia que todos os cretenses eram mentirosos. A afirmação poderia até parecer simples, mas se fosse verdade que todos os de Creta mentiam, então Epimênides, que era cretense, não estaria dizendo a verdade.
E no caso contrário, se a afirmação de que todos mentem fosse falsa, a afirmação de Epimênides acabaria sendo verdadeira, mas sendo ele cretense, a frase deveria ser considerada mentirosa.
3. Paradoxo de Abilene

Esse paradoxo social foi proposto por Jerry B. Harvey, em seu livro O paradoxo de Abilene e outras meditações sobre a administração (em tradução livre). No exemplo, uma família está jogando dominó na varanda. Estão presentes os sogros e um casal.
O sogro sugere que eles se dirijam a Abilene, localidade situada a 80km de onde eles estavam. A esposa diz que viajar seria uma boa ideia, apesar de não estar totalmente convencida, pois fazia muito calor e ela pensava que ninguém concordaria com ela. O marido também aceita, presumindo que sua sogra está com muita vontade de ir. Assim, eles acabam pegando a estrada. Como a esposa havia previsto, o trajeto foi longo, quente e cansativo.
A refeição no restaurante que eles visitam não cai bem, e eles resolvem voltar para casa depois de algumas horas. No caminho de volta, a esposa diz, em tom sarcástico, que a viagem não tinha sido muito boa. O marido responde dizendo que ele só tinha aceitado viajar para agradar a sogra, que não havia se manifestado sobre o assunto, enquanto o sogro diz ter sugerido a viagem porque todo mundo parecia entediado.
Eles ficam perplexos ao perceber que tomaram em conjunto a decisão de fazer algo que ninguém queria. Assim, Harvey tentou explicar como algumas situações nos obrigam a fazer coisas que não são necessariamente a nossa vontade.
4. O gato de Schrödinger
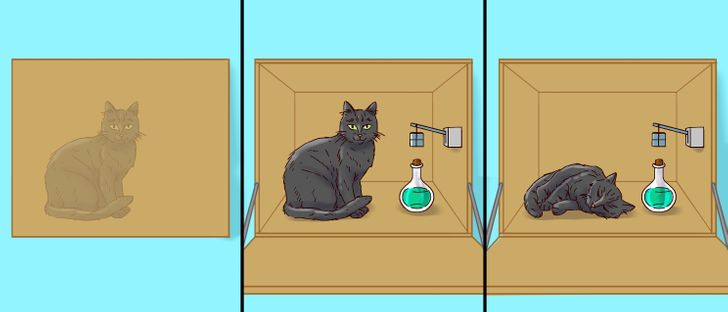
O físico austríaco Erwin Schrödinger criou um sistema composto por uma caixa opaca onde havia um recipiente com veneno, um dispositivo com uma única partícula radioativa com 50% de probabilidades de explodir, e um gato. Assim, o gato tem 50% de possibilidade de sobreviver dentro da caixa.
Os elétrons têm a capacidade de estar em dois lugares ao mesmo tempo, como os receptores que indicam se o gato está vivo ou morto, mostrando ambos os resultados simultaneamente. Não obstante, só ao abrir a caixa é possível verificar se o gato morreu ou não. Enquanto a caixa está fechada, ambas as afirmações são corretas, caracterizando o paradoxo.
5. Paradoxo do avô

Esse dilema, também conhecido como paradoxo da viagem no tempo, foi pensado pelo autor de obras de ficção científica René Barjavel, em 1943, como parte de seu romance O Viajante Imprudente. Nele, questiona-se o que aconteceria se um homem viajasse ao passado e matasse o próprio avô, pai de seu pai biológico.
Se o avô morre no passado, então o próprio homem jamais nasceria. Portanto, não é possível saber quem mataria o avô nesse contexto. Assim, talvez o avô sobrevivesse, possibilitando o nascimento do viajante, e assim sucessivamente.
6. Paradoxo do barbeiro

Esse paradoxo tem também um outro nome: “paradoxo de Rusell”. Ele demonstra a teoria dos conjuntos e é atribuído a Bertrand Rusell, filósofo, matemático e escritor. O dilema narra a história de As-Samet, barbeiro de um antigo emirado, que tinha muita habilidade para cuidar de barbas e cabelos. Um dia, o emir determinou que, diante da falta de barbeiros, os barbeiros existentes só deveriam barbear os homens que não pudessem se barbear por conta própria.
Enquanto As-Samet barbeava o emir, contava a ele que, no afã de cumprir a determinação, encontrou-se diante de um grande dilema. Ele era o único barbeiro da localidade, e não poderia barbear a si mesmo, já que, segundo a lei, ele estava impedido de fazer a própria barba por ser o único barbeiro do emirado. Aos olhos do emir, aquela reflexão foi tão profunda que ele resolveu dar a As-Samet a mão de uma de suas filhas em casamento.
7. Paradoxo dos gêmeos

Foi proposto por Albert Einstein para explicar a teoria da relatividade, estabelecendo que a medida do tempo não é absoluta, pois depende do movimento e da perspectiva do espectador. O paradoxo usa a história de dois gêmeos: um deles faria uma longa viagem espacial, sob alta velocidade, enquanto o outro continuaria na Terra por cerca de 20 anos.
O paradoxo estabelece que o gêmeo que ficou em casa envelhecerá mais rápido por conta da dilatação do tempo, ou seja, por ele ver o tempo passando mais lentamente. Por outro lado, o gêmeo que partiu na nave espacial voltará parecendo mais jovem, já que, por ter viajado em alta velocidade, enxergará o tempo correndo mais rapidamente. Tudo isso porque o tempo é relativo.
8. O hotel infinito de Hilbert

Para explicar os fatos paradoxais dentro do conceito matemático do infinito, Hilbert utilizou como exemplo a história de dois grandes empresários do setor hoteleiro que tinham como ambição construir o maior hotel do mundo. Diante da questão envolvendo o número de quartos do empreendimento, eles chegaram à conclusão de que, se alguém construísse um hotel com maior capacidade de alojamento, logo seu estabelecimento deixaria de ser o maior do mundo. Por isso, eles resolvem construir um hotel com número infinito de quartos.
Quando o hotel inaugurou, fez muito sucesso, de modo que os infinitos quartos passaram a ser ocupados por infinitos hóspedes, e não havia espaço para receber mais nenhum. Para resolver o dilema e evitar que algum cliente ficasse sem quarto, os responsáveis pediram que cada hóspede somasse 1 ao número de seu quarto, e se mudasse para a unidade correspondente. Assim, a pessoa do quarto 1 se mudaria para o de número 2, o do 2 iria para o 3, e assim sucessivamente, de forma que o quarto de número 1 ficasse disponível.
Tempos depois, chegaram infinitos hóspedes e, mais uma vez, não houve problemas para alojar a todos. A cada cliente foi pedido que multiplicasse por dois o número do respectivo quarto, de modo que todos ocupassem uma suíte de número par. Assim, os infinitos hóspedes ocupariam os infinitos números ímpares.
9. Dilema do crocodilo

Esse dilema foi usado para trazer à luz os problemas de lógica envolvendo aquilo que ainda não conhecemos, mas que temos certa noção do que pode acontecer. O paradoxo é ilustrado com a história de um crocodilo que arranca um menino dos braços de sua mãe. O animal promete à mulher que devolverá seu filho, desde que ela adivinhe o que ele fará com a criança.
A mãe responde que o bicho vai devorar a criança, criando um dilema para o réptil. Se o crocodilo decide comer o menino, estará quebrando sua promessa, já que a mãe acertou a adivinhação. Logo, a criança deveria ser devolvida. Já no caso de o crocodilo resolver entregar a criança, a mãe estaria equivocada, mas da mesma forma teria seu filho de volta.
10. O navio de Teseu

De acordo com a lenda grega, Teseu voltava de Creta rumo a Atenas na companhia de vários jovens. Eles estavam em um navio de trinta remos que tinha sido mantido por várias gerações e estava em bom estado, já que cada parte danificada era logo substituída por uma nova.
Isso fez com que filósofos passassem a discutir se o navio era o mesmo ou se a frequente substituição de peças fizera dele uma embarcação diferente. Eles se perguntaram: se as peças do barco original tinham sido trocadas, qual seria então o navio de Teseu? O que foi reformado com o passar dos anos ou cada uma das peças velhas?
Você conhece outro paradoxo capaz de nos deixar refletindo por horas? Acha que tem a solução para alguma das questões apresentadas acima? Deixe um comentário com as suas conclusões!
Comentários
????????? demais p mim !! kkkk
????? muito bom
Artigos relacionados
8 Truques para lidar com pessoas que tentam nos menosprezar

17 Pessoas que tentaram encontrar seus amores, mas os encontros não saíram como o esperado

17 Ilustrações que brincam com o seu cérebro

10 Problemas de saúde causados pela falta de contato com amigos

16 Internautas que já erraram a idade de alguém e acabaram em situações constrangedoras

9 Truques psicológicos que você pode começar a aplicar agora mesmo

18 Provas de que algumas mulheres têm fotos “nada recomendáveis” para as redes sociais

10 Filhos de celebridades brasileiras que têm uma beleza peculiar

Como responder perguntas para que não voltem a fazê-las

15 Pessoas que descobriram um segredo obscuro de família

15 Pessoas cuja aparência parece ter sido feita com efeitos especiais

Gastei mais de US$ 100.000 em cirurgias plásticas para me transformar em Britney Spears
