Os 3 enigmas mais difíceis que você resolverá neste ano

Tenho alguns enigmas para você hoje, mas esses são difíceis, então ligue o motor do seu cérebro e vamos lá!

Era uma vez uma floresta mágica habitada por elfos e gnomos. Como eles não se davam muito bem, viviam em duas partes diferentes da floresta para evitar qualquer conflito. Um dia, os centauros invadiram a floresta, e os elfos e gnomos foram forçados a sair, correndo em direções diferentes.
Vamos seguir um pequeno grupo de seis criaturas: três elfos e três gnomos. Eles correram para o oeste, mas, infelizmente, deram de cara com um lago. Nenhum deles sabia nadar, mas, por sorte, havia uma jangada.
A jangada só podia carregar duas criaturas de uma vez: dois elfos, dois gnomos ou um elfo e um gnomo. Portanto, você precisa descobrir uma maneira de todos eles atravessarem o lago em segurança.
O problema é o seguinte: se houver mais gnomos em um lado do que elfos, eles os atacarão. Mesmo que um elfo esteja na jangada, mas na parte do lago onde há mais gnomos do que elfos, ainda assim não é seguro. Você consegue descobrir uma maneira de todos atravessarem o lago em segurança?

Então, aqui estão cinco possíveis primeiros passos.
Um elfo atravessa o lago, ou um gnomo, ou dois elfos, dois gnomos, ou um elfo e um gnomo. Mas não faz sentido atravessar o lago sozinho, já que eles precisam enviar a jangada de volta de alguma forma, então essas duas opções estão fora de cogitação. Dois elfos não podem atravessar o lago juntos porque o terceiro elfo ficará sozinho com três gnomos e eles o atacarão. Portanto, ou dois gnomos atravessam o lago primeiro ou um elfo e um gnomo.
Vamos optar por dois gnomos. Então, dois deles atravessam o lago e, é claro, um deles tem de voltar. E agora? Dois elfos não podem sair porque o terceiro estará em perigo. Se um elfo e um gnomo partirem juntos, aquele que está partindo estará em perigo assim que cruzar o rio. Então, mais dois gnomos partem juntos. E então um volta. Um elfo e um gnomo não podem sair juntos, porque então haverá três gnomos e um elfo do outro lado. Então, dessa vez, dois elfos atravessam o lago juntos. Quem volta? Não um elfo, porque o outro não pode ficar sozinho lá. Um gnomo não pode voltar sozinho — caso contrário, haverá dois gnomos e um elfo na primeira margem.

Então, uma reviravolta na trama: um elfo e um gnomo voltam a se unir. Agora, dois gnomos não podem atravessar o lago. Um elfo e um gnomo também não podem ir. Então, os dois elfos restantes vão juntos para a outra margem. Agora, nenhum deles pode retornar, pois há dois gnomos restantes naquela margem. Então, um gnomo voltará para buscar um de seus companheiros. Depois, outro gnomo irá buscar o último gnomo. Mas essa não é a única solução. Você também poderia ter sucesso enviando um gnomo e um elfo juntos como primeira jogada.

Ok, ótimo trabalho! Agora é hora do segundo enigma, e este vem de Esme.

Essa garota costuma sair para caminhar em uma floresta e, normalmente, se perde. Desta vez, porém, ela não se perde. Aqui está o caminho de casa — mas ela se sente tentada a visitar sua velha amiga, uma bruxa, que vive na floresta. Esme tem um enigma incrível, e é bem difícil. Por isso, ela acha que tem uma boa chance de ganhar o gato da bruxa. Então, Esme vai até a casa da bruxa e diz o seguinte:"Aposto que você não consegue resolver meu enigma. Se eu estiver certa, seu gato irá comigo“. A bruxa acredita que pode resolver qualquer enigma, então ela assume o risco. Esme coloca um grande triângulo agudo sobre a mesa. “Aqui está. Você pode fazer sete cortes para fazer esse triângulo desaparecer. Todo pedaço que você cortar que for um triângulo agudo desaparecerá. Mas, se um triângulo tiver um ângulo reto ou obtuso, essa peça permanecerá. Mais uma vez — sete cortes, e você terá que fazer o triângulo inteiro desaparecer; nem um único pedaço menor pode ser deixado”. Como a bruxa pode fazer isso e manter seu gato?

Sempre que você fizer um corte, ele produzirá dois ângulos retos ou um ângulo agudo e um obtuso. A bruxa parece estar condenada, mas então ela olha para a pizza que ainda não terminou. Quando você corta em mais de quatro pedaços, todos os ângulos são agudos. O problema é que a pizza é redonda, e estamos lidando com um triângulo. Mesmo assim. O truque também funciona com outras formas, como hexágonos e pentágonos. Bom para a bruxa — ela pode criar um pentágono a partir desse triângulo agudo fazendo apenas dois cortes. Os pequenos triângulos cortados são agudos e desaparecem. Agora, a bruxa precisa lidar com o pentágono como faz com uma pizza: cortá-lo em cinco pedaços, usando os últimos cinco cortes. Essa é uma história de sucesso! Sabemos que você gosta do gato, Esme, mas talvez você possa ter o seu próprio gato.

Ok, você acha que consegue resolver mais um? Prometo que é a última de hoje, e é bem divertida, sem mais geometria.

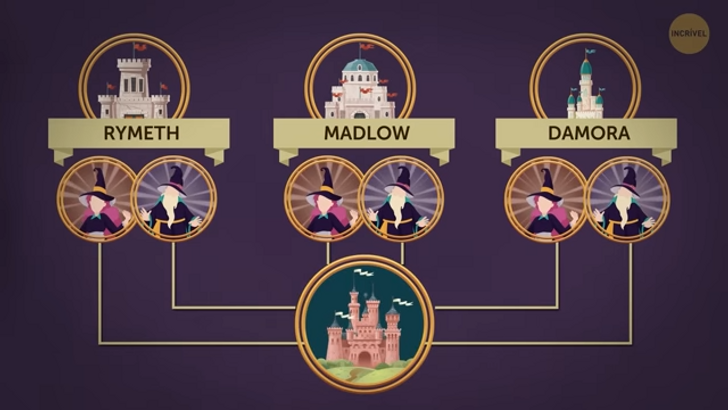
A história é a seguinte: há mil anos, seis irmãos fundaram uma escola mágica. Ingram, Regala e Corona são bruxos, e Agnard, Ardumo e Modnor são magos. Dois irmãos fundaram uma casa cada, e os nomes dessas casas são Rymeth, Madlow e Damora. Todos os seis também fundaram a quarta casa, que recebeu o nome do sétimo irmão que desapareceu quando eles eram jovens.

Você é convidado a estudar em uma escola mágica. Mas, ao chegar, precisa ser classificado em sua casa. Você precisa colocar a mão sobre o livro de classificação e esperar que a decisão dele se ilumine na capa. Quando você faz isso, o livro vê potencial em você. Então, em vez de classificá-lo imediatamente em uma das três casas, ele lhe dá a oportunidade de entrar na quarta casa, para onde vão os jovens mágicos mais talentosos. Para provar que você é bom o suficiente para ser classificado nessa casa, você precisa resolver o enigma da classificação. A tarefa é adivinhar o nome da casa especial, que ninguém além de seus alunos conhece. Mas você tem algumas orientações que podem servir como dicas.
Primeiro, você precisa descobrir quem fundou qual casa. Aqui estão algumas observações.
— Cada casa foi fundada por um irmão e uma irmã.
— Corona e Regala fundaram Rymeth e Madlow (mas não necessariamente nessa ordem).
— Ingram e Ardumo fundaram Madlow e Damora (mas não necessariamente nessa ordem).
— Agnard e Regala fundaram a mesma casa.
Depois de descobrir isso, a próxima etapa é adivinhar o nome da casa secreta. Para revelá-la, descubra o que todos os irmãos têm em comum. E então, você é talentoso o suficiente para ser classificado naquela casa especial?

Primeiro, você precisa descobrir quem fundou cada casa. Portanto, o par é sempre um irmão e uma irmã. Vamos dar uma olhada nas condições dois e três. Cada uma delas menciona Madlow. Tanto Corona quanto Regala são irmãs, o que significa que, independentemente de quem fundou a Madlow, ela já tem uma irmã fundadora. Portanto, Ingram, que também é uma bruxa, não poderia ter fundado essa casa. O que significa que a Madlow foi fundada por Ardumo. Portanto, Ingram fundou a Damora. Agnard fundou a mesma casa com Regala, portanto foi Modnor quem fundou Damora com Ingram. Portanto, só nos resta Rymeth para Agnard e Regala. Finalmente, Corona fundou Madlow.

Muito bem, ótimo. Agora temos que descobrir o nome da quinta casa. O que os irmãos têm em comum? É claro que todos eles têm a letra “R” em seus nomes. Vamos colocá-los em ordem de aparecimento da letra em seus nomes, começando por Regala. Abaixo de cada um de seus nomes, vamos colocar o nome da casa que eles fundaram. Agora, as respectivas letras sob cada “R” formam o nome Radota. Esse é o nome de sua irmã desaparecida, e é assim que a quarta casa se chama. Então, amigo, se você descobriu, parabéns — e bem-vindo ao lar.